Different Computational Problems

انواع مسائل محاسباتی

مسائلی که به آن‌ها بر‌ می‌خوریم را می‌توان از لحاظ محاسباتی به چند کلاس تقسیم کرد. آن دسته از مسائلی را که الگوریتم‌‌های حل آن‌‌ها برای تعداد ورودی  شامل تعداد مراحلی برابر با توانی ثابت از n² (یا مثلا n³) باشد، مسائل کلاس P یا Polynomial می‌نامند. کامپیوترهای کلاسیک تنها قادر به حل این دسته از مسائل به صورت کارآمد هستند. منظور از کارآمدی به طور ساده، استفاده از زمان/منابع به اندازه کافی منطقی (با توجه به اندازه‌ی ورودی n ) است. این در حالی است که مسائل بسیار مهم دیگری وجود دارند که درون کلاس دیگری به نام NP یا Non-Polynomial قرار داشته و خارج از محدوده‌ی P قرار می‌گیرند؛ یعنی با کامپیوترهای کلاسیک نمی‌توان با صرف زمان یا منابع منطقی آن‌ها را به صورت کارآمد حل کرد. ویژگی بارز این دسته از مسائل آن است که حل آن‌ها به زمان/منابع در مقیاس فراتر از چندجمله‌ای نیاز دارد اما زمان/منابع لازم برای چک کردن یک جواب داده شده برای آن ها هنوز یک چندجمله‌ای می‌باشد.

ثابت شده است که اگر نگاهمان را به رایانش از نوع منطق کلاسیک آن به منطقی تازه، یعنی منطق کوانتومی، تغییر دهیم، پاره‌ای از مسائل کلاس NP را می‌توانیم به صورت کارآمد حل کنیم. این مسائل شامل الگوریتم‌های فاکتورگیری، جستجو، بهینه‌سازی، و پاره‌ای دیگر از عملیات رایانشی هستند.

رایانش‌های کوانتومی مدلی نویدبخش برای افزایش نمایی سرعت بعضی از مسائل مربوطه مانند فاکتورگیری، پیدا کردن لگاریتم گسسته، حل معادله Pell، حل مسائل زیرگروه­های مخفی و سامانه­های فیزیکی شبیه سازی شده است. این مسائل کاربردهایی در سامانه­های رمزی کلید عمومی و مدل­سازی سامانه­های کوانتومی مانند فیزیک انرژی­های بالا و سامانه­های ماده چگال دارد. دیگر کاربرد مهم الگوریتم‌های کوانتومی فهم مدل­های شیمی کوانتومی است که زمینه طراحی مرغوب داروها و تحلیل اثر آن­ها را فراهم می­آورد. این مسائل شامل پیدا کردن برخورد است که معادلات مختلفی را با استفاده از روش عناصر محدود حل می­کند و روی گراف­ها برای نشان دادن راس­ها جست­وجو می­کند.

کلاس P مجموع‌ه­ای از مسائل تصمیمی است (یعنی مسائلی با پاسخ بله یا خیر) که در این گونه مسائل با توجه به اندازه ورودی، می‌توان به طور قطع مسئله را در یک ساختار چند مرحله‌ای که تعداد مراحل آن یک چند جمله‌ای از n تعداد ورودی است حل نمود.

نمونه کوانتومی P با QPB نشان داده می­شود و مربوط به زمان چندجمله­ای کوانتومی کراندار است. این مسائل تصمیمی است که می­تواند در زمان چندجمله‌­ای روی کامپیوترهای کوانتومی حل شود. از آنجایی که QPB شامل P است، مشخص نیست که آیا همه‌ی مسائل خارج از P در دامنه QPB می‌تواند قرار بگیرد یا خیر. دلیل مستقیمی وجود ندارد که ثابت کند QPB شامل تمام NP می‌شود. البته ناگفته نماند که ممکن است کامپیوترهای کوانتومی قادر به حل مسائلی حتی پیچیده تر از مسائل NP باشند.

برخی مسائل گروه NP را اصطلاحا NP-Complete می گویند. این دسته از مسائل به گونه‌ای هستند که در صورتی که کامپیوتری قابلیت حل یکی از آن ها را به صورت کارآمد داشته باشد، قابل اثبات است که آن کامپیوتر می تواند تمامی مسائل NP دیگر را نیز به صورت کارآمد حل کند. به عبارت دیگر، هنگامی که یک مسئله  کامل است تمامی مسائل NP دیگر می­توانند به آن کاهش یابند. این بدان معنی است که اگر بتوانیم یک مسئله کامل  را حل کنیم، هر مسئله دیگری در  را با جایگزینی یک چندجمله‌­ای می­توانیم حل کنیم. برای این جایگزینی نیاز است که راه­‌حل یک مسئله به راه‌­حل مسائل دیگر تبدیل شود. به این دلیل مسائل کامل  سخت­ترین مسائل کلاس  هستند. اگرچه چند مسئله وجود دارد که به سختی مسائل  است یعنی راه­‌حل آن، به عنوان راه‌­حل هر مسئله  قرار می‌گیرد. اما این­ها مسائل تصمیمی نیستند. به عنوان مثال پیدا کردن یک راه­‌حل برای مسائل قیدی اقناعی (CSP) نسبت به تصمیمی، اگر راه‌­حلی وجود داشته باشد یا نداشته باشد، یکی از مسائلی است که در  قرار ندارد. این مسائل، مسائل سخت  نامیده می­­‌شوند. بسیاری از مسائل که در تمرین­‌ها با آن مواجه می­‌شویم مسائل تصمیمی نیستند که ما راه­‌حل آن یا حداقل بعضی از خصوصیات راه­­حلش را بدانیم. این کلاس PH نامیده میشود.

مشابه مرتبه‌های چند جمله ای، مرتبه‌های دیگری به نام مرتبه‌های نمایی وجود دارد. این دسته از مسائل بر پایه کلاس های NXP و NXEP هستند که به ترتیب مخفف محاسبه زمان نمایی قطعی و غیر قطعی است. این کلاس ها مشابه‌های زمانی نمایی P و  NP می‌باشند.

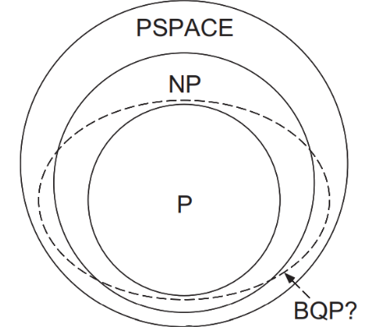
نموداری از کلاس‌های مختلف مسائل در علم کامپیوتر و محاسبات و دامنه‌ای که کامپیوترهای کوانتومی قادرند تا مسائل غیرقابل حل با کامپیوترهای کلاسیک را به صورت کارآمد حل کنند.